Introduction
This article explains how to compute the main descriptive statistics in R and how to present them graphically.
Descriptive statistics is a branch of statistics aiming at summarizing, describing and presenting a series of values or a dataset. Descriptive statistics is often the first step and an important part in any statistical analysis. It allows to check the quality of the data and it helps to “understand” the data by having a clear overview of it. If well presented, descriptive statistics is already a good starting point for further analyses.
Here, we focus only on the implementation in R of the most common descriptive statistics and their visualizations (when deemed appropriate).
Data
We use the dataset iris throughout the article. If you would like to know about the iris data, you can type:
help(iris)This dataset is imported by default in R, you only need to load it by running iris:
dat <- iris # load the iris dataset and renamed it datBelow a preview of this dataset and its structure:
head(dat) # first 6 observations## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosastr(dat) # structure of dataset## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...The dataset contains 150 observations and 5 variables, representing the length and width of the sepal and petal and the species of 150 flowers. Length and width of the sepal and petal are numeric variables and the species is a factor with 3 levels (indicated by num and Factor w/ 3 levels after the name of the variables). (Remenber the different variables types in R in the lecture).
Regarding plots, we present the default graphs and the graphs from the well-known {ggplot2} package. Graphs from the {ggplot2} package usually have a better look but it requires more advanced coding skills (see the article “Graphics in R with ggplot2” to learn more). If you need to publish or share your graphs, I suggest using {ggplot2} if you can, otherwise the default graphics will do the job.
Tip: I recently discovered the ggplot2 builder from the {esquisse} addins. See how you can easily draw graphs from the {ggplot2} package without having to code it yourself.
All plots displayed in this article can be customized. For instance, it is possible to edit the title, x and y-axis labels, color, etc. However, customizing plots is beyond the scope of this article so all plots are presented without any customization. Interested readers will find numerous resources online.
Minimum and maximum
Minimum and maximum can be found thanks to the min() and max() functions:
min(dat$Sepal.Length)## [1] 4.3max(dat$Sepal.Length)## [1] 7.9Alternatively the range() function:
rng <- range(dat$Sepal.Length)
rng## [1] 4.3 7.9gives you the minimum and maximum directly. Note that the output of the range() function is actually an object containing the minimum and maximum (in that order). This means you can actually access the minimum with:
rng[1] # rng = name of the object specified above## [1] 4.3and the maximum with:
rng[2]## [1] 7.9This reminds us that, in R, there are often several ways to arrive at the same result. The method that uses the shortest piece of code is usually preferred as a shorter piece of code is less prone to coding errors and more readable.
Range
The range can then be easily computed, as you have guessed, by subtracting the minimum from the maximum:
max(dat$Sepal.Length) - min(dat$Sepal.Length)## [1] 3.6To my knowledge, there is no default function to compute the range. However, if you are familiar with writing functions in R , you can create your own function to compute the range:
range2 <- function(x) {
range <- max(x) - min(x)
return(range)
}
range2(dat$Sepal.Length)## [1] 3.6which is equivalent than presented above.
Mean
The mean can be computed with the mean() function:
mean(dat$Sepal.Length)## [1] 5.843333Tips:
- if there is at least one missing value in your dataset, use
mean(dat$Sepal.Length, na.rm = TRUE)to compute the mean with the NA excluded. This argument can be used for most functions presented in this article, not only the mean - for a truncated mean, use
mean(dat$Sepal.Length, trim = 0.10)and change thetrimargument to your needs
Median
The median can be computed thanks to the median() function:
median(dat$Sepal.Length)## [1] 5.8or with the quantile() function:
quantile(dat$Sepal.Length, 0.5)## 50%
## 5.8since the quantile of order 0.5 () corresponds to the median.
First and third quartile
As the median, the first and third quartiles can be computed thanks to the quantile() function and by setting the second argument to 0.25 or 0.75:
quantile(dat$Sepal.Length, 0.25) # first quartile## 25%
## 5.1quantile(dat$Sepal.Length, 0.75) # third quartile## 75%
## 6.4You may have seen that the results above are slightly different than the results you would have found if you compute the first and third quartiles by hand. It is normal, there are many methods to compute them (R actually has 7 methods to compute the quantiles!). However, the methods presented here and in the article “descriptive statistics by hand” are the easiest and most “standard” ones. Furthermore, results do not dramatically change between the two methods.
Other quantiles
As you have guessed, any quantile can also be computed with the quantile() function. For instance, the decile or the percentile:
quantile(dat$Sepal.Length, 0.4) # 4th decile## 40%
## 5.6quantile(dat$Sepal.Length, 0.98) # 98th percentile## 98%
## 7.7Interquartile range
The interquartile range (i.e., the difference between the first and third quartile) can be computed with the IQR() function:
IQR(dat$Sepal.Length)## [1] 1.3or alternatively with the quantile() function again:
quantile(dat$Sepal.Length, 0.75) - quantile(dat$Sepal.Length, 0.25)## 75%
## 1.3As mentioned earlier, when possible it is usually recommended to use the shortest piece of code to arrive at the result. For this reason, the IQR() function is preferred to compute the interquartile range.
Standard deviation and variance
The standard deviation and the variance is computed with the sd() and var() functions:
sd(dat$Sepal.Length) # standard deviation## [1] 0.8280661var(dat$Sepal.Length) # variance## [1] 0.6856935Remember from the article descriptive statistics by hand that the standard deviation and the variance are different whether we compute it for a sample or a population (see the difference between sample and population). In R, the standard deviation and the variance are computed as if the data represent a sample (so the denominator is , where is the number of observations). To my knowledge, there is no function by default in R that computes the standard deviation or variance for a population.
Tip: to compute the standard deviation (or variance) of multiple variables at the same time, use lapply() with the appropriate statistics as second argument:
lapply(dat[, 1:4], sd)## $Sepal.Length
## [1] 0.8280661
##
## $Sepal.Width
## [1] 0.4358663
##
## $Petal.Length
## [1] 1.765298
##
## $Petal.Width
## [1] 0.7622377The command dat[, 1:4] selects the variables 1 to 4 as the fifth variable is a qualitative variable and the standard deviation cannot be computed on such type of variable. See a recap of the different data types in R if needed.
Summary
You can compute the minimum, quartile, median, mean, quartile and the maximum for all numeric variables of a dataset at once using summary():
summary(dat)## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
## Species
## setosa :50
## versicolor:50
## virginica :50
##
##
## Tip: if you need these descriptive statistics by group use the by() function:
by(dat, dat$Species, summary)## dat$Species: setosa
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.300 Min. :1.000 Min. :0.100
## 1st Qu.:4.800 1st Qu.:3.200 1st Qu.:1.400 1st Qu.:0.200
## Median :5.000 Median :3.400 Median :1.500 Median :0.200
## Mean :5.006 Mean :3.428 Mean :1.462 Mean :0.246
## 3rd Qu.:5.200 3rd Qu.:3.675 3rd Qu.:1.575 3rd Qu.:0.300
## Max. :5.800 Max. :4.400 Max. :1.900 Max. :0.600
## Species
## setosa :50
## versicolor: 0
## virginica : 0
##
##
##
## ------------------------------------------------------------
## dat$Species: versicolor
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.900 Min. :2.000 Min. :3.00 Min. :1.000 setosa : 0
## 1st Qu.:5.600 1st Qu.:2.525 1st Qu.:4.00 1st Qu.:1.200 versicolor:50
## Median :5.900 Median :2.800 Median :4.35 Median :1.300 virginica : 0
## Mean :5.936 Mean :2.770 Mean :4.26 Mean :1.326
## 3rd Qu.:6.300 3rd Qu.:3.000 3rd Qu.:4.60 3rd Qu.:1.500
## Max. :7.000 Max. :3.400 Max. :5.10 Max. :1.800
## ------------------------------------------------------------
## dat$Species: virginica
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.900 Min. :2.200 Min. :4.500 Min. :1.400
## 1st Qu.:6.225 1st Qu.:2.800 1st Qu.:5.100 1st Qu.:1.800
## Median :6.500 Median :3.000 Median :5.550 Median :2.000
## Mean :6.588 Mean :2.974 Mean :5.552 Mean :2.026
## 3rd Qu.:6.900 3rd Qu.:3.175 3rd Qu.:5.875 3rd Qu.:2.300
## Max. :7.900 Max. :3.800 Max. :6.900 Max. :2.500
## Species
## setosa : 0
## versicolor: 0
## virginica :50
##
##
## where the arguments are the name of the dataset, the grouping variable and the summary function. Follow this order, or specify the name of the arguments if you do not follow this order.
If you need more descriptive statistics, use stat.desc() from the package {pastecs}:
library(pastecs)
stat.desc(dat)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## nbr.val 150.00000000 150.00000000 150.0000000 150.00000000 NA
## nbr.null 0.00000000 0.00000000 0.0000000 0.00000000 NA
## nbr.na 0.00000000 0.00000000 0.0000000 0.00000000 NA
## min 4.30000000 2.00000000 1.0000000 0.10000000 NA
## max 7.90000000 4.40000000 6.9000000 2.50000000 NA
## range 3.60000000 2.40000000 5.9000000 2.40000000 NA
## sum 876.50000000 458.60000000 563.7000000 179.90000000 NA
## median 5.80000000 3.00000000 4.3500000 1.30000000 NA
## mean 5.84333333 3.05733333 3.7580000 1.19933333 NA
## SE.mean 0.06761132 0.03558833 0.1441360 0.06223645 NA
## CI.mean.0.95 0.13360085 0.07032302 0.2848146 0.12298004 NA
## var 0.68569351 0.18997942 3.1162779 0.58100626 NA
## std.dev 0.82806613 0.43586628 1.7652982 0.76223767 NA
## coef.var 0.14171126 0.14256420 0.4697441 0.63555114 NAYou can have even more statistics (i.e., skewness, kurtosis and normality test) by adding the argument norm = TRUE in the previous function. Note that the variable Species is not numeric, so descriptive statistics cannot be computed for this variable and NA are displayed.
Coefficient of variation
The coefficient of variation can be found with stat.desc() (see the line coef.var in the table above) or by computing manually (remember that the coefficient of variation is the standard deviation divided by the mean):
sd(dat$Sepal.Length) / mean(dat$Sepal.Length)## [1] 0.1417113Mode
To my knowledge there is no function to find the mode of a variable. However, we can easily find it thanks to the functions table() and sort():
tab <- table(dat$Sepal.Length) # number of occurrences for each unique value
sort(tab, decreasing = TRUE) # sort highest to lowest##
## 5 5.1 6.3 5.7 6.7 5.5 5.8 6.4 4.9 5.4 5.6 6 6.1 4.8 6.5 4.6 5.2 6.2 6.9 7.7
## 10 9 9 8 8 7 7 7 6 6 6 6 6 5 5 4 4 4 4 4
## 4.4 5.9 6.8 7.2 4.7 6.6 4.3 4.5 5.3 7 7.1 7.3 7.4 7.6 7.9
## 3 3 3 3 2 2 1 1 1 1 1 1 1 1 1table() gives the number of occurrences for each unique value, then sort() with the argument decreasing = TRUE displays the number of occurrences from highest to lowest. The mode of the variable Sepal.Length is thus 5. This code to find the mode can also be applied to qualitative variables such as Species:
sort(table(dat$Species), decreasing = TRUE)##
## setosa versicolor virginica
## 50 50 50or:
summary(dat$Species)## setosa versicolor virginica
## 50 50 50Contingency table
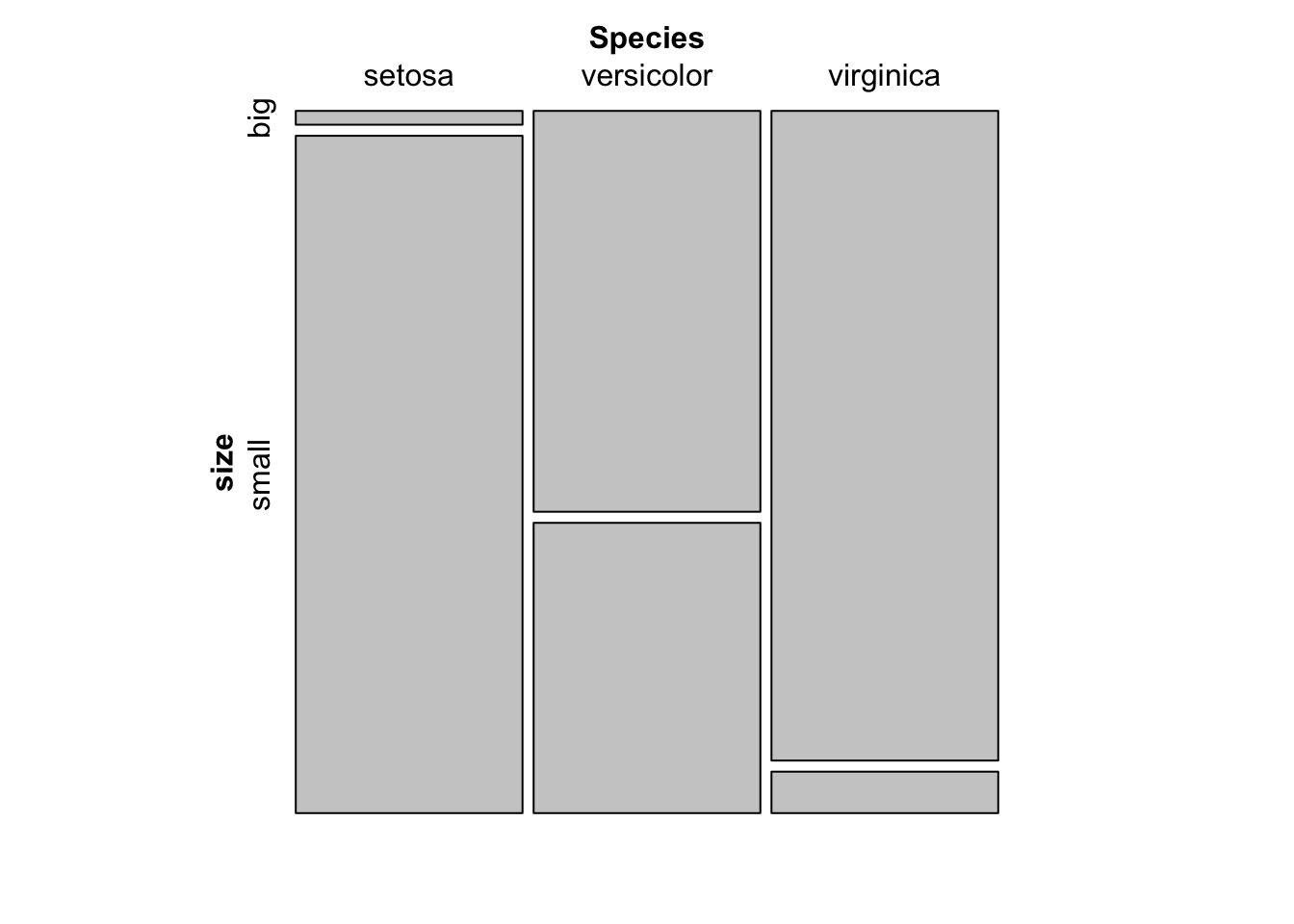
table() introduced above can also be used on two qualitative variables to create a contingency table. The dataset iris has only one qualitative variable so we create a new qualitative variable just for this example. We create the variable size which corresponds to small if the length of the petal is smaller than the median of all flowers, big otherwise:
dat$size <- ifelse(dat$Sepal.Length < median(dat$Sepal.Length),
"small", "big"
)Here is a recap of the occurrences by size:
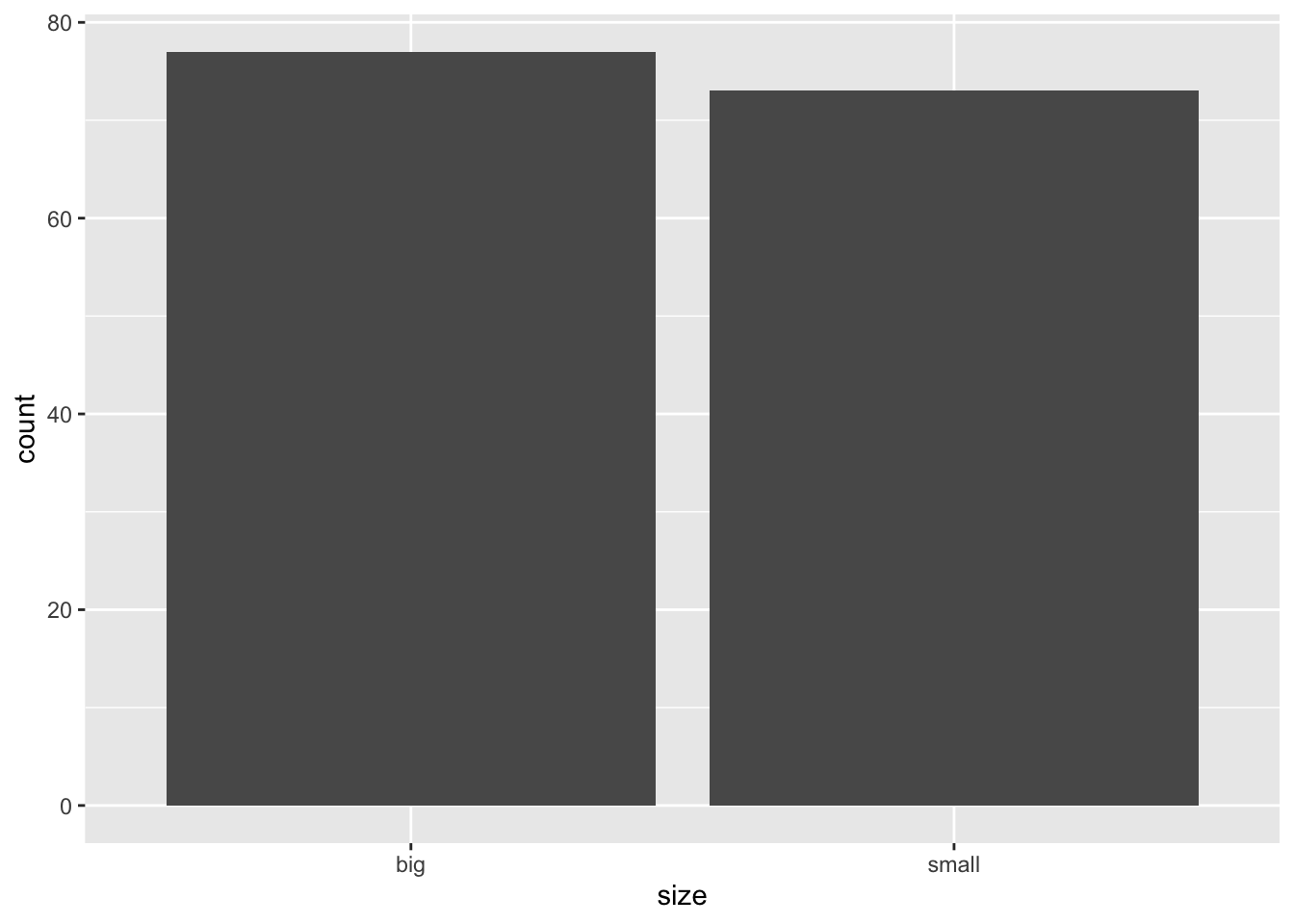
table(dat$size)##
## big small
## 77 73We now create a contingency table of the two variables Species and size with the table() function:
table(dat$Species, dat$size)##
## big small
## setosa 1 49
## versicolor 29 21
## virginica 47 3or with the xtabs() function:
xtabs(~ dat$Species + dat$size)## dat$size
## dat$Species big small
## setosa 1 49
## versicolor 29 21
## virginica 47 3The contingency table gives the number of cases in each subgroup. For instance, there is only one big setosa flower, while there are 49 small setosa flowers in the dataset.
To go further, we can see from the table that setosa flowers seem to be larger in size than virginica flowers. In order to check whether size is significantly associated with species, we could perform a Chi-square test of independence since both variables are categorical variables. See how to do this test by hand and in R.
Note that Species are in rows and size in column because we specified Species and then size in table(). Change the order if you want to switch the two variables.
Instead of having the frequencies (i.e.. the number of cases) you can also have the relative frequencies (i.e., proportions) in each subgroup by adding the table() function inside the prop.table() function:
prop.table(table(dat$Species, dat$size))##
## big small
## setosa 0.006666667 0.326666667
## versicolor 0.193333333 0.140000000
## virginica 0.313333333 0.020000000Note that you can also compute the percentages by row or by column by adding a second argument to the prop.table() function: 1 for row, or 2 for column:
# percentages by row:
round(prop.table(table(dat$Species, dat$size), 1), 2) # round to 2 digits with round()##
## big small
## setosa 0.02 0.98
## versicolor 0.58 0.42
## virginica 0.94 0.06# percentages by column:
round(prop.table(table(dat$Species, dat$size), 2), 2) # round to 2 digits with round()##
## big small
## setosa 0.01 0.67
## versicolor 0.38 0.29
## virginica 0.61 0.04Barplot
Barplots can only be done on qualitative variables (remember the difference with a quantitative variable). A barplot is a tool to visualize the distribution of a qualitative variable. We draw a barplot of the qualitative variable size:
barplot(table(dat$size)) # table() is mandatoryHistogram
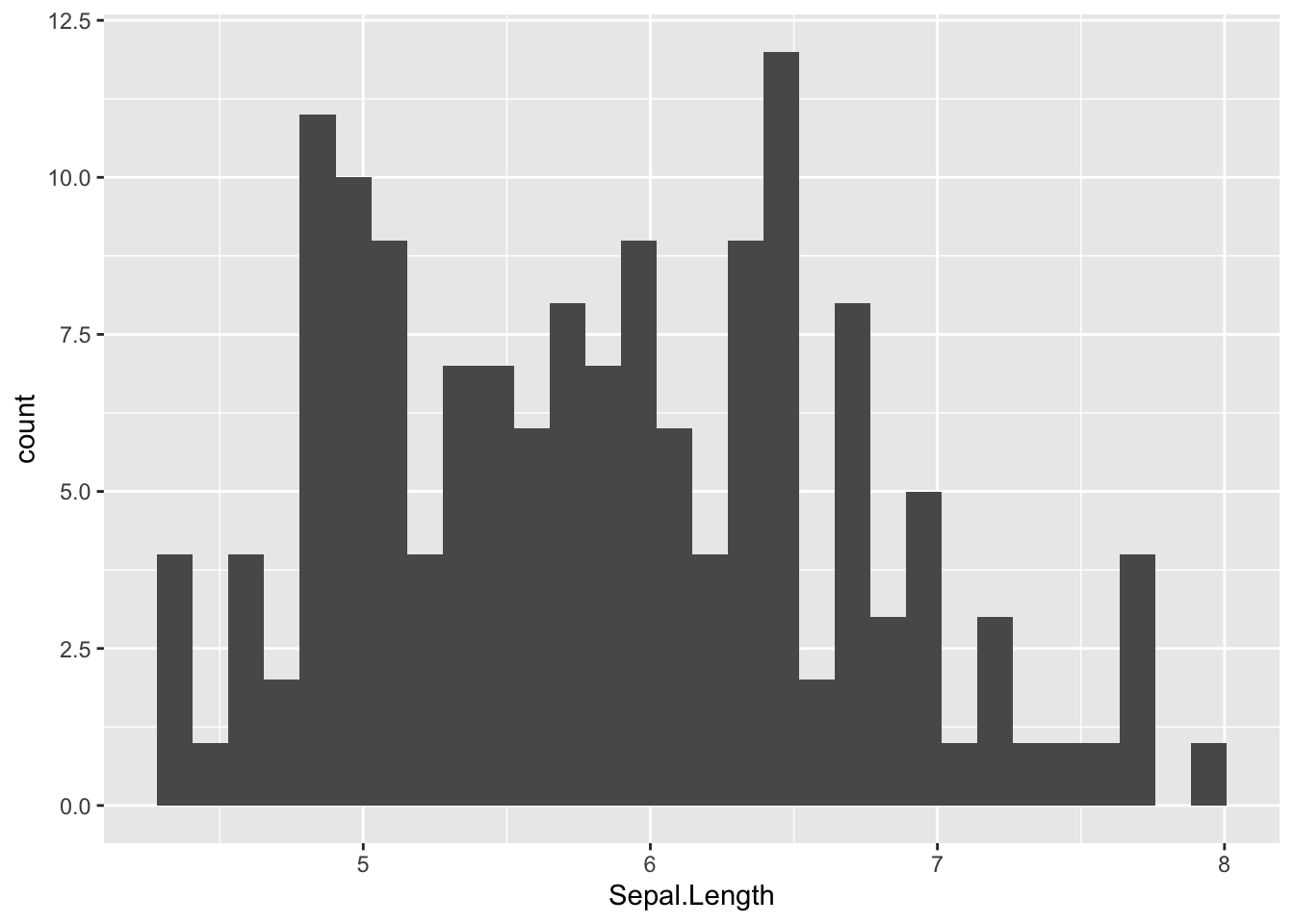
A histogram gives an idea about the distribution of a quantitative variable. The idea is to break the range of values into intervals and count how many observations fall into each interval. Histograms are a bit similar to barplots, but histograms are used for quantitative variables whereas barplots are used for qualitative variables. To draw a histogram in R, use hist():
hist(dat$Sepal.Length)Boxplot
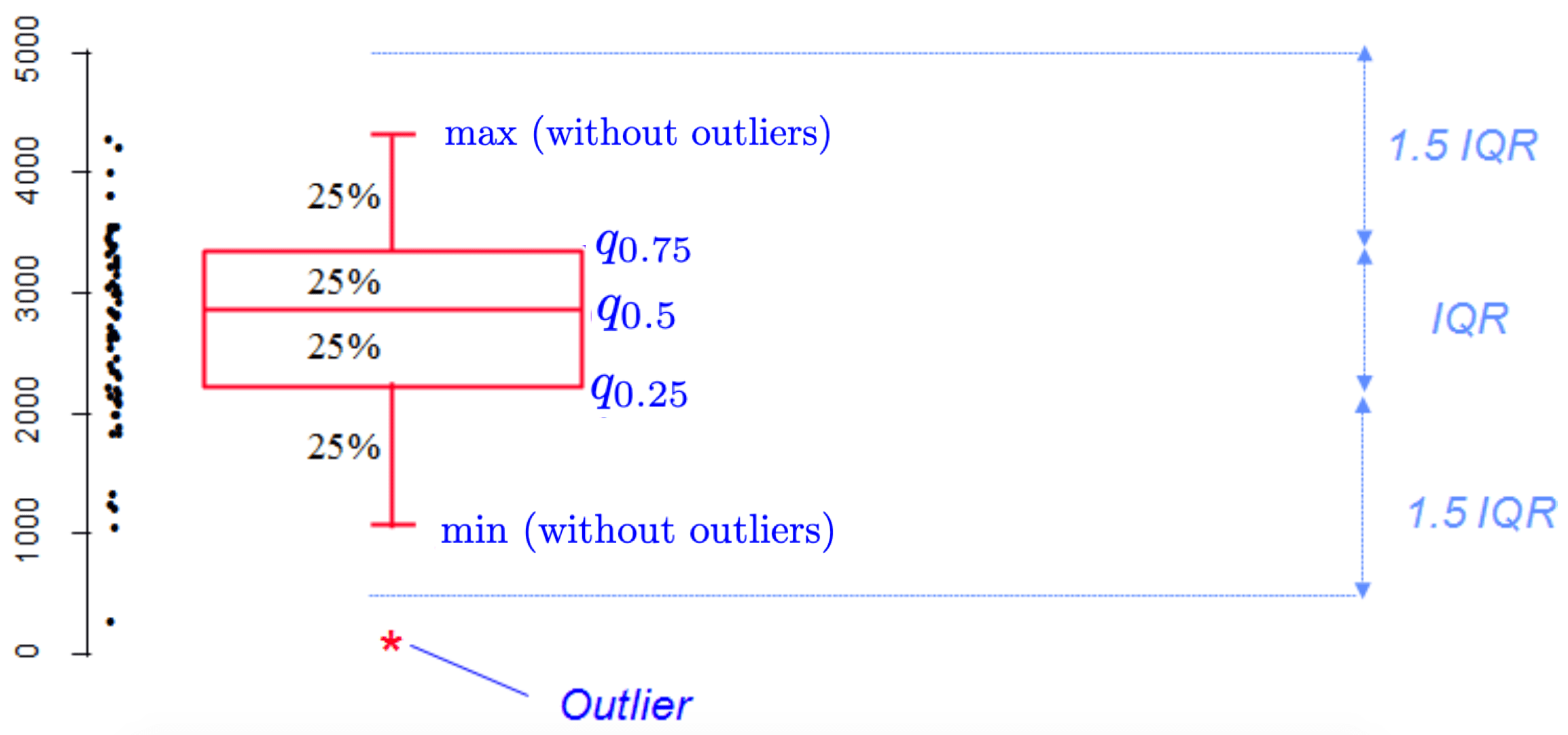
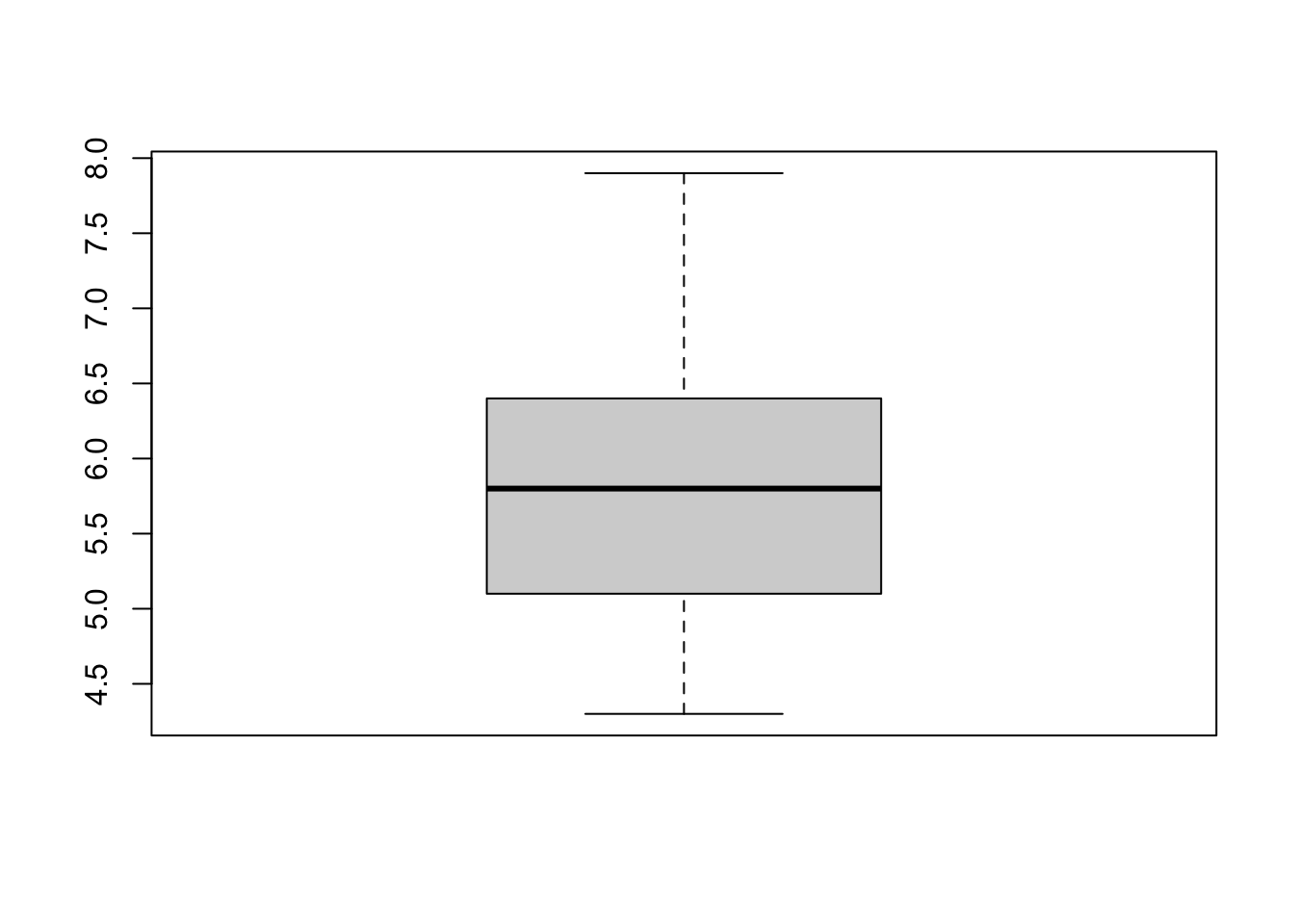
Boxplots are really useful in descriptive statistics and are often underused (mostly because it is not well understood by the public). A boxplot graphically represents the distribution of a quantitative variable by visually displaying five common location summary (minimum, median, first/third quartiles and maximum) and any observation that was classified as a suspected outlier using the interquartile range (IQR) criterion. The IQR criterion means that all observations above or below (where and correspond to first and third quartile respectively) are considered as potential outliers by R. The minimum and maximum in the boxplot are represented without these suspected outliers.
Seeing all these information on the same plot help to have a good first overview of the dispersion and the location of the data. Before drawing a boxplot of our data, see below a graph explaining the information present on a boxplot:
Now an example with our dataset:
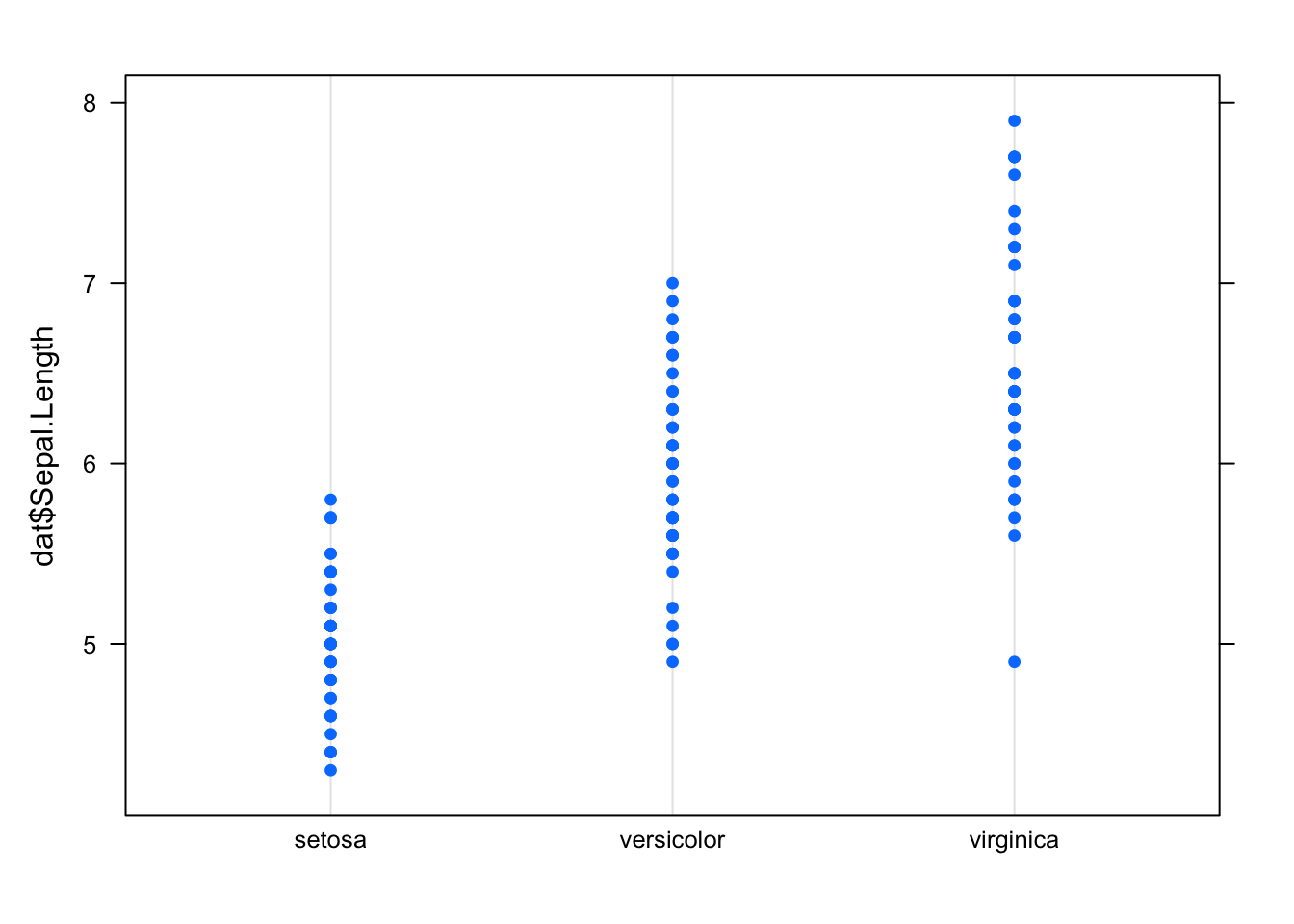
boxplot(dat$Sepal.Length)Boxplots are even more informative when presented side-by-side for comparing and contrasting distributions from two or more groups. For instance, we compare the length of the sepal across the different species:
boxplot(dat$Sepal.Length ~ dat$Species)Scatterplot
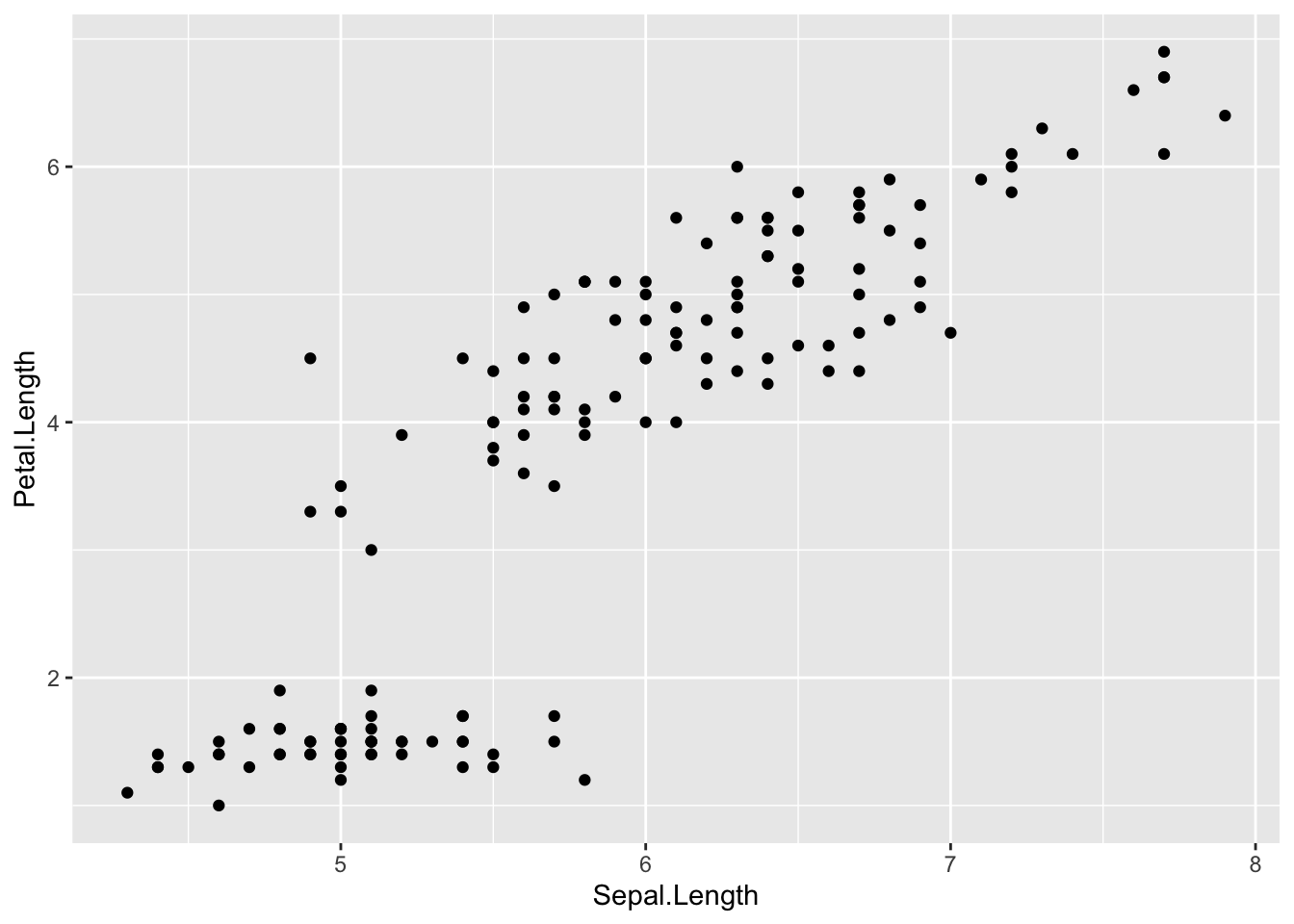
Scatterplots allow to check whether there is a potential link between two quantitative variables. For this reason, scatterplots are often used to visualize a potential correlation between two variables. For instance, when drawing a scatterplot of the length of the sepal and the length of the petal:
plot(dat$Sepal.Length, dat$Petal.Length)There seems to be a positive association between the two variables.
0 comments:
Post a Comment