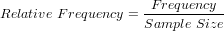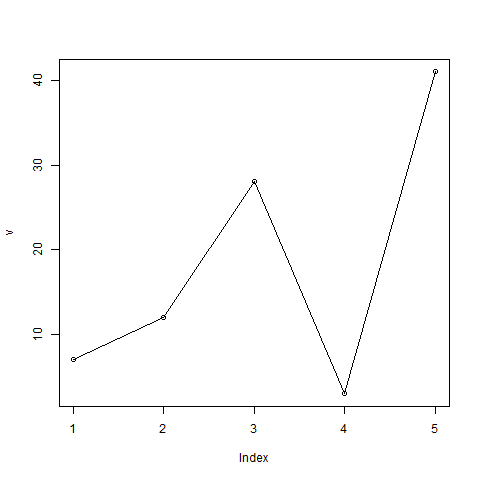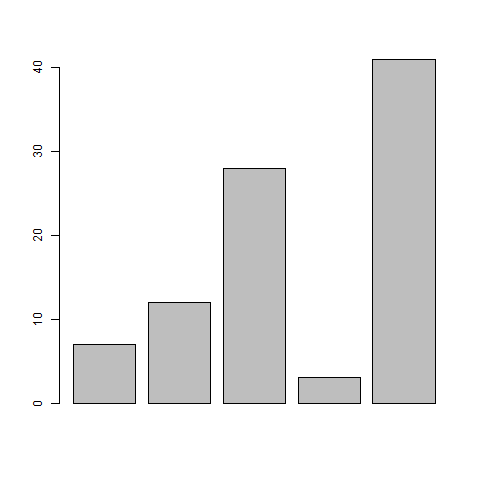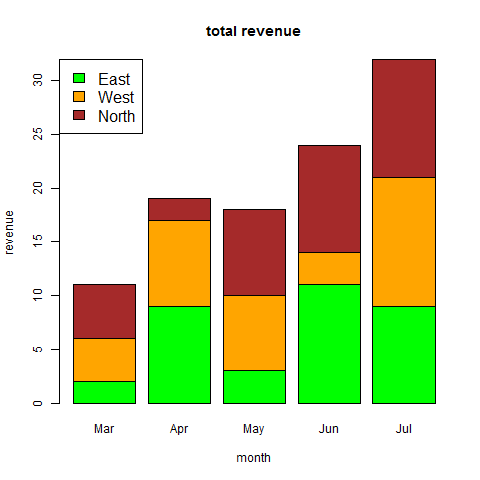Pertemuan ke-3 Numerical Measures

Mean

The mean of an observation variable is a numerical measure of the central location of the data values. It is the sum of its data values divided by data count.

Hence, for a data sample of size n, its sample mean is defined as follows:

Similarly, for a data population of size N, the population mean is:

Problem

Find the mean eruption duration in the data set faithful.

Solution

We apply the mean function to compute the mean value of eruptions.

> duration = faithful$eruptions     # the eruption durations 
> mean(duration)                    # apply the mean function 
[1] 3.4878

Answer

The mean eruption duration is 3.4878 minutes.

Exercise

Find the mean eruption waiting periods in faithful.

Median

The median of an observation variable is the value at the middle when the data is sorted in ascending order. It is an ordinal measure of the central location of the data values.

Problem

Find the median of the eruption duration in the data set faithful.

Solution

We apply the median function to compute the median value of eruptions.

> duration = faithful$eruptions     # the eruption durations 
> median(duration)                  # apply the median function 
[1] 4

Answer

The median of the eruption duration is 4 minutes.

Exercise

Find the median of the eruption waiting periods in faithful.

Quartile

There are several quartiles of an observation variable. The first quartile, or lower quartile, is the value that cuts off the first 25% of the data when it is sorted in ascending order. The second quartile, or median, is the value that cuts off the first 50%. The third quartile, or upper quartile, is the value that cuts off the first 75%.

Problem

Find the quartiles of the eruption durations in the data set faithful.

Solution

We apply the quantile function to compute the quartiles of eruptions.

> duration = faithful$eruptions     # the eruption durations 
> quantile(duration)                # apply the quantile function 
    0%    25%    50%    75%   100% 
1.6000 2.1627 4.0000 4.4543 5.1000

Answer

The first, second and third quartiles of the eruption duration are 2.1627, 4.0000 and 4.4543 minutes respectively.

Exercise

Find the quartiles of the eruption waiting periods in faithful.

Note

There are several algorithms for the computation of quartiles. Details can be found in the R documentation via help(quantile).

Percentile

The n^th percentile of an observation variable is the value that cuts off the first n percent of the data values when it is sorted in ascending order.

Problem

Find the 32^nd, 57^th and 98^th percentiles of the eruption durations in the data set faithful.

Solution

We apply the quantile function to compute the percentiles of eruptions with the desired percentage ratios.

> duration = faithful$eruptions     # the eruption durations 
> quantile(duration, c(.32, .57, .98)) 
   32%    57%    98% 
2.3952 4.1330 4.9330

Answer

The 32^nd, 57^th and 98^th percentiles of the eruption duration are 2.3952, 4.1330 and 4.9330 minutes respectively.

Exercise

Find the 17^th, 43^rd, 67^th and 85^th percentiles of the eruption waiting periods in faithful.

Note

There are several algorithms for the computation of percentiles. Details can be found in the R documentation via help(quantile).

Range

The range of an observation variable is the difference of its largest and smallest data values. It is a measure of how far apart the entire data spreads in value.

Problem

Find the range of the eruption duration in the data set faithful.

Solution

We apply the max and min function to compute the largest and smallest values of eruptions, then take the difference.

> duration = faithful$eruptions     # the eruption durations 
> max(duration) − min(duration)     # apply the max and min functions 
[1] 3.5

Answer

The range of the eruption duration is 3.5 minutes.

Exercise

Find the range of the eruption waiting periods in faithful.

Interquartile Range

The interquartile range of an observation variable is the difference of its upper and lower quartiles. It is a measure of how far apart the middle portion of data spreads in value.

Problem

Find the interquartile range of eruption duration in the data set faithful.

Solution

We apply the IQR function to compute the interquartile range of eruptions.

> duration = faithful$eruptions     # the eruption durations 
> IQR(duration)                     # apply the IQR function 
[1] 2.2915

Answer

The interquartile range of eruption duration is 2.2915 minutes.

Exercise

Find the interquartile range of eruption waiting periods in faithful.

Box Plot

The box plot of an observation variable is a graphical representation based on its quartiles, as well as its smallest and largest values. It attempts to provide a visual shape of the data distribution.

Problem

Find the box plot of the eruption duration in the data set faithful.

Solution

We apply the boxplot function to produce the box plot of eruptions.

> duration = faithful$eruptions       # the eruption durations 
> boxplot(duration, horizontal=TRUE)  # horizontal box plot

Answer

The box plot of the eruption duration is:

Exercise

Find the box plot of the eruption waiting periods in faithful.

Variance

The variance is a numerical measure of how the data values is dispersed around the mean. In particular, the sample variance is defined as:

Similarly, the population variance is defined in terms of the population mean μ and population size N:

Problem

Find the variance of the eruption duration in the data set faithful.

Solution

We apply the var function to compute the variance of eruptions.

> duration = faithful$eruptions    # the eruption durations 
> var(duration)                    # apply the var function 
[1] 1.3027

Answer

The variance of the eruption duration is 1.3027.

Exercise

Find the variance of the eruption waiting periods in faithful.

Standard Deviation

The standard deviation of an observation variable is the square root of its variance.

Problem

Find the standard deviation of the eruption duration in the data set faithful.

Solution

We apply the sd function to compute the standard deviation of eruptions.

> duration = faithful$eruptions    # the eruption durations 
> sd(duration)                     # apply the sd function 
[1] 1.1414

Answer

The standard deviation of the eruption duration is 1.1414.

Exercise

Find the standard deviation of the eruption waiting periods in faithful.

Covariance

The covariance of two variables x and y in a data set measures how the two are linearly related. A positive covariance would indicate a positive linear relationship between the variables, and a negative covariance would indicate the opposite.

The sample covariance is defined in terms of the sample means as:

Similarly, the population covariance is defined in terms of the population mean μ_x, μ_y as:

Problem

Find the covariance of eruption duration and waiting time in the data set faithful. Observe if there is any linear relationship between the two variables.

Solution

We apply the cov function to compute the covariance of eruptions and waiting.

> duration = faithful$eruptions   # eruption durations 
> waiting = faithful$waiting      # the waiting period 
> cov(duration, waiting)          # apply the cov function 
[1] 13.978

Answer

The covariance of eruption duration and waiting time is about 14. It indicates a positive linear relationship between the two variables.

Correlation Coefficient

The correlation coefficient of two variables in a data set equals to their covariance divided by the product of their individual standard deviations. It is a normalized measurement of how the two are linearly related.

Formally, the sample correlation coefficient is defined by the following formula, where s_x and s_y are the sample standard deviations, and s_xy is the sample covariance.

Similarly, the population correlation coefficient is defined as follows, where σ_x and σ_y are the population standard deviations, and σ_xy is the population covariance.

If the correlation coefficient is close to 1, it would indicate that the variables are positively linearly related and the scatter plot falls almost along a straight line with positive slope. For -1, it indicates that the variables are negatively linearly related and the scatter plot almost falls along a straight line with negative slope. And for zero, it would indicate a weak linear relationship between the variables.

Problem

Find the correlation coefficient of eruption duration and waiting time in the data set faithful. Observe if there is any linear relationship between the variables.

Solution

We apply the cor function to compute the correlation coefficient of eruptions and waiting.

> duration = faithful$eruptions   # eruption durations 
> waiting = faithful$waiting      # the waiting period 
> cor(duration, waiting)          # apply the cor function 
[1] 0.90081

Answer

The correlation coefficient of eruption duration and waiting time is 0.90081. Since it is rather close to 1, we can conclude that the variables are positively linearly related.

Central Moment

The k^th central moment (or moment about the mean) of a data population is:

Similarly, the k^th central moment of a data sample is:

In particular, the second central moment of a population is its variance.

Problem

Find the third central moment of eruption duration in the data set faithful.

Solution

We apply the function moment from the e1071 package. As it is not in the core R library, the package has to be installed and loaded into the R workspace.

> library(e1071)                    # load e1071 
> duration = faithful$eruptions     # eruption durations 
> moment(duration, order=3, center=TRUE) 
[1] -0.6149

Answer

The third central moment of eruption duration is -0.6149.

Exercise

Find the third central moment of eruption waiting period in faithful.

Skewness

The skewness of a data population is defined by the following formula, where μ₂ and μ₃ are the second and third central moments.

Intuitively, the skewness is a measure of symmetry. As a rule, negative skewness indicates that the mean of the data values is less than the median, and the data distribution is left-skewed. Positive skewness would indicate that the mean of the data values is larger than the median, and the data distribution is right-skewed.

Problem

Find the skewness of eruption duration in the data set faithful.

Solution

We apply the function skewness from the e1071 package to compute the skewness coefficient of eruptions. As the package is not in the core R library, it has to be installed and loaded into the R workspace.

> library(e1071)                    # load e1071 
> duration = faithful$eruptions     # eruption durations 
> skewness(duration)                # apply the skewness function 
[1] -0.41355

Answer

The skewness of eruption duration is -0.41355. It indicates that the eruption duration distribution is skewed towards the left.

Exercise

Find the skewness of eruption waiting period in faithful.

Pertemuan ke-2: Descriptive Statistics in R (charts)

 

Qualitative Data

A data sample is called qualitative, also known as categorical, if its values belong to a collection of known defined non-overlapping classes. Common examples include student letter grade (A, B, C, D or F), commercial bond rating (AAA, AAB, ...) and consumer clothing shoe sizes (1, 2, 3, ...).

The tutorials in this section are based on an R built-in data frame named painters. It is a compilation of technical information of a few eighteenth century classical painters. The data set belongs to the MASS package, and has to be pre-loaded into the R workspace prior to its use.

> library(MASS)      # load the MASS package 
> painters 
              Composition Drawing Colour Expression School 
Da Udine               10       8     16          3      A 
Da Vinci               15      16      4         14      A 
Del Piombo              8      13     16          7      A 
Del Sarto              12      16      9          8      A 
Fr. Penni               0      15      8          0      A 
Guilio Romano          15      16      4         14      A 
                    .................

The last School column contains the information of school classification of the painters. The schools are named as A, B, ..., etc, and the School variable is qualitative.

> painters$School 
 [1] A A A A A A A A A A B B B B B B C C C C C C D D D D 
[27] D D D D D D E E E E E E E F F F F G G G G G G G H H 
[53] H H 
Levels: A B C D E F G H

Qualitative Data

A data sample is called qualitative, also known as categorical, if its values belong to a collection of known defined non-overlapping classes. Common examples include student letter grade (A, B, C, D or F), commercial bond rating (AAA, AAB, ...) and consumer clothing shoe sizes (1, 2, 3, ...).

The tutorials in this section are based on an R built-in data frame named painters. It is a compilation of technical information of a few eighteenth century classical painters. The data set belongs to the MASS package, and has to be pre-loaded into the R workspace prior to its use.

> library(MASS)      # load the MASS package 
> painters 
              Composition Drawing Colour Expression School 
Da Udine               10       8     16          3      A 
Da Vinci               15      16      4         14      A 
Del Piombo              8      13     16          7      A 
Del Sarto              12      16      9          8      A 
Fr. Penni               0      15      8          0      A 
Guilio Romano          15      16      4         14      A 
                    .................

The last School column contains the information of school classification of the painters. The schools are named as A, B, ..., etc, and the School variable is qualitative.

> painters$School 
 [1] A A A A A A A A A A B B B B B B C C C C C C D D D D 
[27] D D D D D D E E E E E E E F F F F G G G G G G G H H 
[53] H H 
Levels: A B C D E F G H

For further details of the painters data set, please consult the R documentation.

> help(painters)

Frequency Distribution of Qualitative Data

The frequency distribution of a data variable is a summary of the data occurrence in a collection of non-overlapping categories.

Example

In the data set painters, the frequency distribution of the School variable is a summary of the number of painters in each school.

Problem

Find the frequency distribution of the painter schools in the data set painters.

Solution

We apply the table function to compute the frequency distribution of the School variable.

> library(MASS)                 # load the MASS package 
> school = painters$School      # the painter schools 
> school.freq = table(school)   # apply the table function

Answer

The frequency distribution of the schools is:

> school.freq 
school 
 A  B  C  D  E  F  G  H 
10  6  6 10  7  4  7  4

Enhanced Solution

We apply the cbind function to print the result in column format.

> cbind(school.freq) 
  school.freq 
A          10 
B           6 
C           6 
D          10 
E           7 
F           4 
G           7 
H           4

Relative Frequency Distribution of Qualitative Data

The relative frequency distribution of a data variable is a summary of the frequency proportion in a collection of non-overlapping categories.

The relationship of frequency and relative frequency is:

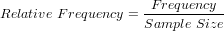
Example

In the data set painters, the relative frequency distribution of the School variable is a summary of the proportion of painters in each school.

Problem

Find the relative frequency distribution of the painter schools in the data set painters.

Solution

We first apply the table function to compute the frequency distribution of the School variable.

> library(MASS)                 # load the MASS package 
> school = painters$School      # the painter schools 
> school.freq = table(school)   # apply the table function

Then we find the sample size of painters with the nrow function, and divide the frequency distribution with it. Therefore the relative frequency distribution is:

> school.relfreq = school.freq / nrow(painters)

Answer

The relative frequency distribution of the schools is:

> school.relfreq 
school 
       A        B        C        D        E        F 
0.185185 0.111111 0.111111 0.185185 0.129630 0.074074 
       G        H 
0.129630 0.074074

Enhanced Solution

We can print with fewer digits and make it more readable by setting the digits option.

> old = options(digits=1) 
> school.relfreq 
school 
   A    B    C    D    E    F    G    H 
0.19 0.11 0.11 0.19 0.13 0.07 0.13 0.07 
> options(old)

In addition, we can apply the cbind function to print the result in column format.

> old = options(digits=1) 
> cbind(school.relfreq) 
  school.relfreq 
A           0.19 
B           0.11 
C           0.11 
D           0.19 
E           0.13 
F           0.07 
G           0.13 
H           0.07 
> options(old)    # restore the old option

Quantitative Data

Quantitative data, also known as continuous data, consists of numeric data that support arithmetic operations. This is in contrast with qualitative data, whose values belong to pre-defined classes with no arithmetic operation allowed. We will explain how to apply some of the R tools for quantitative data analysis with examples.

The tutorials in this section are based on a built-in data frame named faithful. It consists of a collection of observations of the Old Faithful geyser in the USA Yellowstone National Park. The following is a preview via the head function.

> head(faithful) 
  eruptions waiting 
1     3.600      79 
2     1.800      54 
3     3.333      74 
4     2.283      62 
5     4.533      85 
6     2.883      55

There are two observation variables in the data set. The first one, called eruptions, is the duration of the geyser eruptions. The second one, called waiting, is the length of waiting period until the next eruption.

Frequency Distribution of Quantitative Data

The frequency distribution of a data variable is a summary of the data occurrence in a collection of non-overlapping categories.

Example

In the data set faithful, the frequency distribution of the eruptions variable is the summary of eruptions according to some classification of the eruption durations.

Problem

Find the frequency distribution of the eruption durations in faithful.

Solution

The solution consists of the following steps:

1. We first find the range of eruption durations with the range function. It shows that the observed eruptions are between 1.6 and 5.1 minutes in duration.
   > duration = faithful$eruptions 
   > range(duration) 
   [1] 1.6 5.1
2. Break the range into non-overlapping sub-intervals by defining a sequence of equal distance break points. If we round the endpoints of the interval [1.6, 5.1] to the closest half-integers, we come up with the interval [1.5, 5.5]. Hence we set the break points to be the half-integer sequence { 1.5, 2.0, 2.5, ... }.
   > breaks = seq(1.5, 5.5, by=0.5)    # half-integer sequence 
   > breaks 
   [1] 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5
3. Classify the eruption durations according to the half-unit-length sub-intervals with cut. As the intervals are to be closed on the left, and open on the right, we set the right argument as FALSE.
   > duration.cut = cut(duration, breaks, right=FALSE)
4. Compute the frequency of eruptions in each sub-interval with the table function.
   > duration.freq = table(duration.cut)

Answer

The frequency distribution of the eruption duration is:

> duration.freq 
duration.cut 
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5) 
     51      41       5       7      30      73      61 
[5,5.5) 
      4

Enhanced Solution

We apply the cbind function to print the result in column format.

> cbind(duration.freq) 
        duration.freq 
[1.5,2)            51 
[2,2.5)            41 
[2.5,3)             5 
[3,3.5)             7 
[3.5,4)            30 
[4,4.5)            73 
[4.5,5)            61 
[5,5.5)             4

Relative Frequency Distribution of Quantitative Data

The relative frequency distribution of a data variable is a summary of the frequency proportion in a collection of non-overlapping categories.

The relationship of frequency and relative frequency is:

Example

In the data set faithful, the relative frequency distribution of the eruptions variable shows the frequency proportion of the eruptions according to a duration classification.

Problem

Find the relative frequency distribution of the eruption durations in faithful.

Solution

We first find the frequency distribution of the eruption durations as follows. Further details can be found in the Frequency Distribution tutorial.

> duration = faithful$eruptions 
> breaks = seq(1.5, 5.5, by=0.5) 
> duration.cut = cut(duration, breaks, right=FALSE) 
> duration.freq = table(duration.cut)

Then we find the sample size of faithful with the nrow function, and divide the frequency distribution with it. As a result, the relative frequency distribution is:

> duration.relfreq = duration.freq / nrow(faithful)

Answer

The frequency distribution of the eruption variable is:

> duration.relfreq 
duration.cut 
 [1.5,2)  [2,2.5)  [2.5,3)  [3,3.5)  [3.5,4)  [4,4.5) 
0.187500 0.150735 0.018382 0.025735 0.110294 0.268382 
 [4.5,5)  [5,5.5) 
0.224265 0.014706

Enhanced Solution

We can print with fewer digits and make it more readable by setting the digits option.

> old = options(digits=1) 
> duration.relfreq 
duration.cut 
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5) 
   0.19    0.15    0.02    0.03    0.11    0.27    0.22 
[5,5.5) 
   0.01 
> options(old)    # restore the old option

We then apply the cbind function to print both the frequency distribution and relative frequency distribution in parallel columns.

> old = options(digits=1) 
> cbind(duration.freq, duration.relfreq) 
        duration.freq duration.relfreq 
[1.5,2)            51             0.19 
[2,2.5)            41             0.15 
[2.5,3)             5             0.02 
[3,3.5)             7             0.03 
[3.5,4)            30             0.11 
[4,4.5)            73             0.27 
[4.5,5)            61             0.22 
[5,5.5)             4             0.01 
> options(old)    # restore the old option

Cumulative Frequency Distribution

The cumulative frequency distribution of a quantitative variable is a summary of data frequency below a given level.

Example

In the data set faithful, the cumulative frequency distribution of the eruptions variable shows the total number of eruptions whose durations are less than or equal to a set of chosen levels.

Problem

Find the cumulative frequency distribution of the eruption durations in faithful.

Solution

We first find the frequency distribution of the eruption durations as follows. Further details can be found in the Frequency Distribution tutorial.

> duration = faithful$eruptions 
> breaks = seq(1.5, 5.5, by=0.5) 
> duration.cut = cut(duration, breaks, right=FALSE) 
> duration.freq = table(duration.cut)

We then apply the cumsum function to compute the cumulative frequency distribution.

> duration.cumfreq = cumsum(duration.freq)

Answer

The cumulative distribution of the eruption duration is:

> duration.cumfreq 
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5) 
     51      92      97     104     134     207     268 
[5,5.5) 
    272

Enhanced Solution

We apply the cbind function to print the result in column format.

> cbind(duration.cumfreq) 
        duration.cumfreq 
[1.5,2)               51 
[2,2.5)               92 
[2.5,3)               97 
[3,3.5)              104 
[3.5,4)              134 
[4,4.5)              207 
[4.5,5)              268 
[5,5.5)              272

umulative Frequency Graph

A cumulative frequency graph or ogive of a quantitative variable is a curve graphically showing the cumulative frequency distribution.

Example

In the data set faithful, a point in the cumulative frequency graph of the eruptions variable shows the total number of eruptions whose durations are less than or equal to a given level.

Problem

Find the cumulative frequency graph of the eruption durations in faithful.

Solution

We first find the frequency distribution of the eruption durations as follows. Check the previous tutorial on Frequency Distribution for details.

> duration = faithful$eruptions 
> breaks = seq(1.5, 5.5, by=0.5) 
> duration.cut = cut(duration, breaks, right=FALSE) 
> duration.freq = table(duration.cut)

We then compute its cumulative frequency with cumsum, add a starting zero element, and plot the graph.

> cumfreq0 = c(0, cumsum(duration.freq)) 
> plot(breaks, cumfreq0,            # plot the data 
+   main="Old Faithful Eruptions",  # main title 
+   xlab="Duration minutes",        # x−axis label 
+   ylab="Cumulative eruptions")   # y−axis label 
> lines(breaks, cumfreq0)           # join the points

Cumulative Relative Frequency Distribution

The cumulative relative frequency distribution of a quantitative variable is a summary of frequency proportion below a given level.

The relationship between cumulative frequency and relative cumulative frequency is:

Example

In the data set faithful, the cumulative relative frequency distribution of the eruptions variable shows the frequency proportion of eruptions whose durations are less than or equal to a set of chosen levels.

Problem

Find the cumulative relative frequency distribution of the eruption durations in faithful.

Solution

We first find the frequency distribution of the eruption durations as follows. Further details can be found in the Frequency Distribution tutorial.

> duration = faithful$eruptions 
> breaks = seq(1.5, 5.5, by=0.5) 
> duration.cut = cut(duration, breaks, right=FALSE) 
> duration.freq = table(duration.cut)

We then apply the cumsum function to compute the cumulative frequency distribution.

> duration.cumfreq = cumsum(duration.freq)

Then we find the sample size of faithful with the nrow function, and divide the cumulative frequency distribution with it. As a result, the cumulative relative frequency distribution is:

> duration.cumrelfreq = duration.cumfreq / nrow(faithful)

Answer

The cumulative relative frequency distribution of the eruption variable is:

> duration.cumrelfreq 
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5) 
0.18750 0.33824 0.35662 0.38235 0.49265 0.76103 0.98529 
[5,5.5) 
1.00000

Enhanced Solution

We can print with fewer digits and make it more readable by setting the digits option.

> old = options(digits=2) 
> duration.cumrelfreq 
[1.5,2) [2,2.5) [2.5,3) [3,3.5) [3.5,4) [4,4.5) [4.5,5) 
   0.19    0.34    0.36    0.38    0.49    0.76    0.99 
[5,5.5) 
   1.00 
> options(old)    # restore the old option

We then apply the cbind function to print both the cumulative frequency distribution and relative cumulative frequency distribution in parallel columns.

> old = options(digits=2) 
> cbind(duration.cumfreq, duration.cumrelfreq) 
        duration.cumfreq duration.cumrelfreq 
[1.5,2)               51                0.19 
[2,2.5)               92                0.34 
[2.5,3)               97                0.36 
[3,3.5)              104                0.38 
[3.5,4)              134                0.49 
[4,4.5)              207                0.76 
[4.5,5)              268                0.99 
[5,5.5)              272                1.00 
> options(old)

R - Line Graphs

A line chart is a graph that connects a series of points by drawing line segments between them. These points are ordered in one of their coordinate (usually the x-coordinate) value. Line charts are usually used in identifying the trends in data.

The plot() function in R is used to create the line graph.

Syntax

The basic syntax to create a line chart in R is −

plot(v,type,col,xlab,ylab)

Following is the description of the parameters used −

• v is a vector containing the numeric values.

• type takes the value "p" to draw only the points, "l" to draw only the lines and "o" to draw both points and lines.

• xlab is the label for x axis.

• ylab is the label for y axis.

• main is the Title of the chart.

• col is used to give colors to both the points and lines.

Example

A simple line chart is created using the input vector and the type parameter as "O". The below script will create and save a line chart in the current R working directory.

Live Demo

# Create the data for the chart.
v <- c(7,12,28,3,41)

# Give the chart file a name.
png(file = "line_chart.jpg")

# Plot the bar chart. 
plot(v,type = "o")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

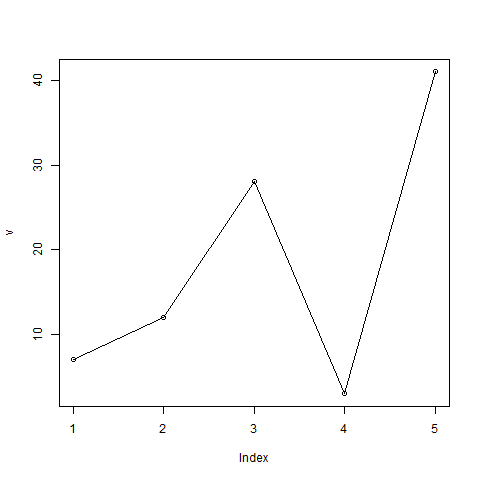
Line Chart Title, Color and Labels

The features of the line chart can be expanded by using additional parameters. We add color to the points and lines, give a title to the chart and add labels to the axes.

Example

Live Demo

# Create the data for the chart.
v <- c(7,12,28,3,41)

# Give the chart file a name.
png(file = "line_chart_label_colored.jpg")

# Plot the bar chart.
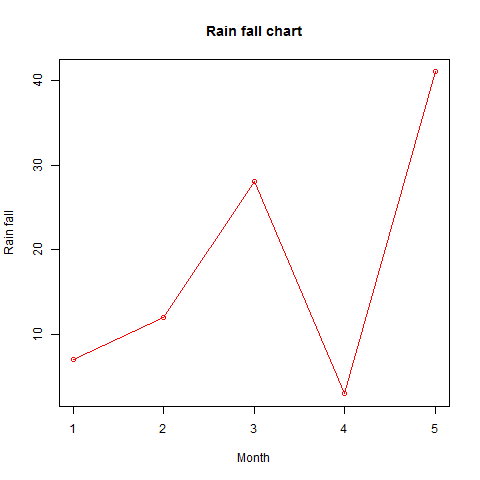
plot(v,type = "o", col = "red", xlab = "Month", ylab = "Rain fall",
   main = "Rain fall chart")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

Multiple Lines in a Line Chart

More than one line can be drawn on the same chart by using the lines()function.

After the first line is plotted, the lines() function can use an additional vector as input to draw the second line in the chart,

Live Demo

# Create the data for the chart.
v <- c(7,12,28,3,41)
t <- c(14,7,6,19,3)

# Give the chart file a name.
png(file = "line_chart_2_lines.jpg")

# Plot the bar chart.
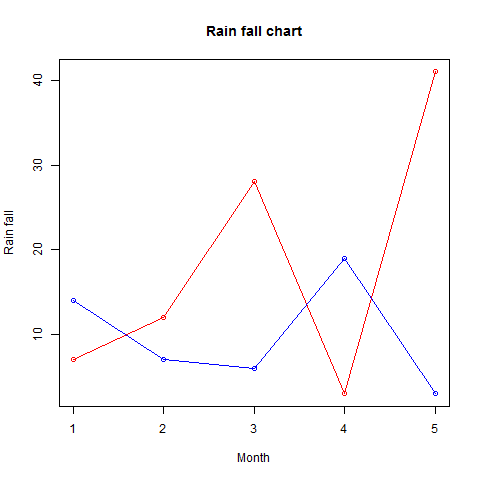
plot(v,type = "o",col = "red", xlab = "Month", ylab = "Rain fall", 
   main = "Rain fall chart")

lines(t, type = "o", col = "blue")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

R - Bar Charts

A bar chart represents data in rectangular bars with length of the bar proportional to the value of the variable. R uses the function barplot() to create bar charts. R can draw both vertical and Horizontal bars in the bar chart. In bar chart each of the bars can be given different colors.

Syntax

The basic syntax to create a bar-chart in R is −

barplot(H,xlab,ylab,main, names.arg,col)

Following is the description of the parameters used −

• H is a vector or matrix containing numeric values used in bar chart.
• xlab is the label for x axis.
• ylab is the label for y axis.
• main is the title of the bar chart.
• names.arg is a vector of names appearing under each bar.
• col is used to give colors to the bars in the graph.

Example

A simple bar chart is created using just the input vector and the name of each bar.

The below script will create and save the bar chart in the current R working directory.

Live Demo

# Create the data for the chart
H <- c(7,12,28,3,41)

# Give the chart file a name
png(file = "barchart.png")

# Plot the bar chart 
barplot(H)

# Save the file
dev.off()

When we execute above code, it produces following result −

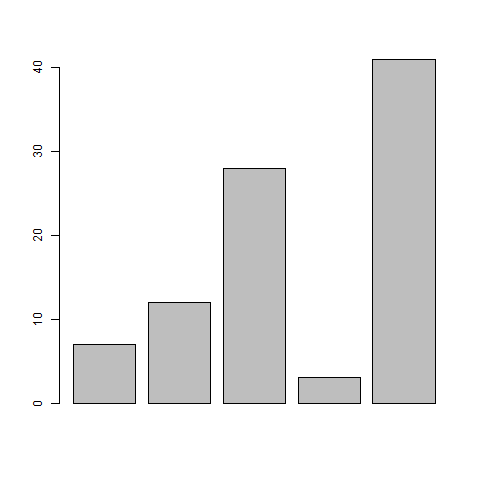
Bar Chart Labels, Title and Colors

The features of the bar chart can be expanded by adding more parameters. The main parameter is used to add title. The col parameter is used to add colors to the bars. The args.name is a vector having same number of values as the input vector to describe the meaning of each bar.

Example

The below script will create and save the bar chart in the current R working directory.

Live Demo

# Create the data for the chart
H <- c(7,12,28,3,41)
M <- c("Mar","Apr","May","Jun","Jul")

# Give the chart file a name
png(file = "barchart_months_revenue.png")

# Plot the bar chart 
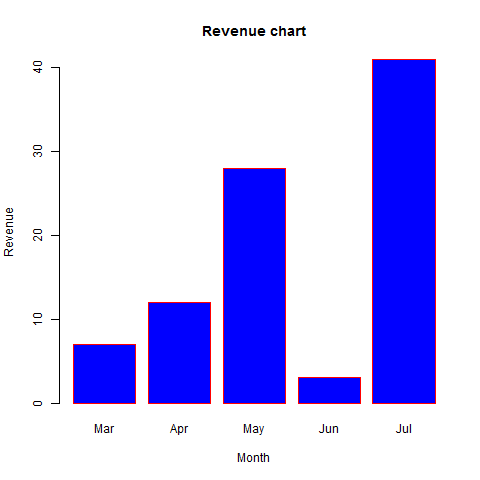
barplot(H,names.arg=M,xlab="Month",ylab="Revenue",col="blue",
main="Revenue chart",border="red")

# Save the file
dev.off()

When we execute above code, it produces following result −

Group Bar Chart and Stacked Bar Chart

We can create bar chart with groups of bars and stacks in each bar by using a matrix as input values.

More than two variables are represented as a matrix which is used to create the group bar chart and stacked bar chart.

# Create the input vectors.
colors = c("green","orange","brown")
months <- c("Mar","Apr","May","Jun","Jul")
regions <- c("East","West","North")

# Create the matrix of the values.
Values <- matrix(c(2,9,3,11,9,4,8,7,3,12,5,2,8,10,11), nrow = 3, ncol = 5, byrow = TRUE)

# Give the chart file a name
png(file = "barchart_stacked.png")

# Create the bar chart
barplot(Values, main = "total revenue", names.arg = months, xlab = "month", ylab = "revenue", col = colors)

# Add the legend to the chart
legend("topleft", regions, cex = 1.3, fill = colors)

# Save the file
dev.off()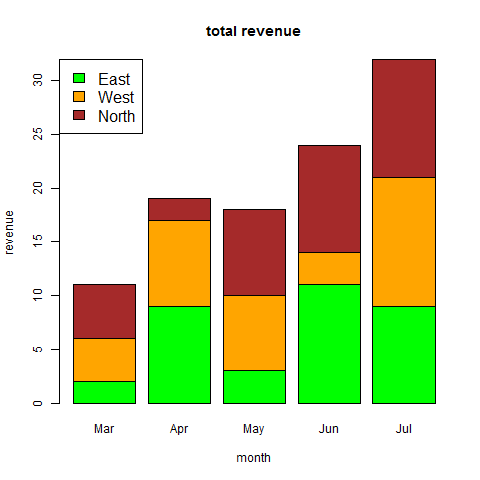

R - Pie Charts

R Programming language has numerous libraries to create charts and graphs. A pie-chart is a representation of values as slices of a circle with different colors. The slices are labeled and the numbers corresponding to each slice is also represented in the chart.

In R the pie chart is created using the pie() function which takes positive numbers as a vector input. The additional parameters are used to control labels, color, title etc.

Syntax

The basic syntax for creating a pie-chart using the R is −

pie(x, labels, radius, main, col, clockwise)

Following is the description of the parameters used −

• x is a vector containing the numeric values used in the pie chart.

• labels is used to give description to the slices.

• radius indicates the radius of the circle of the pie chart.(value between −1 and +1).

• main indicates the title of the chart.

• col indicates the color palette.

• clockwise is a logical value indicating if the slices are drawn clockwise or anti clockwise.

Example

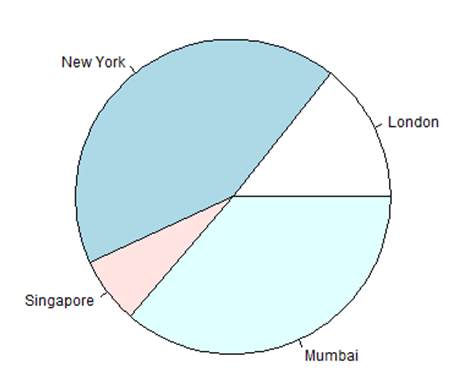
A very simple pie-chart is created using just the input vector and labels. The below script will create and save the pie chart in the current R working directory.

Live Demo

# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")

# Give the chart file a name.
png(file = "city.png")

# Plot the chart.
pie(x,labels)

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

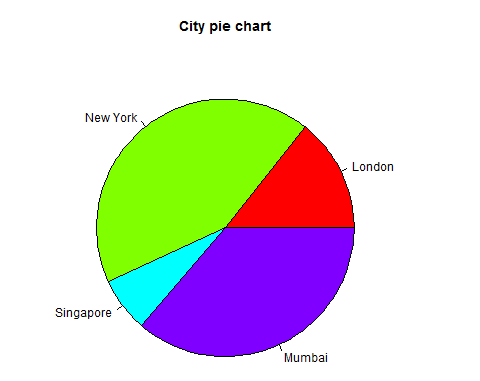
Pie Chart Title and Colors

We can expand the features of the chart by adding more parameters to the function. We will use parameter main to add a title to the chart and another parameter is col which will make use of rainbow colour pallet while drawing the chart. The length of the pallet should be same as the number of values we have for the chart. Hence we use length(x).

Example

The below script will create and save the pie chart in the current R working directory.

Live Demo

# Create data for the graph.
x <- c(21, 62, 10, 53)
labels <- c("London", "New York", "Singapore", "Mumbai")

# Give the chart file a name.
png(file = "city_title_colours.jpg")

# Plot the chart with title and rainbow color pallet.
pie(x, labels, main = "City pie chart", col = rainbow(length(x)))

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

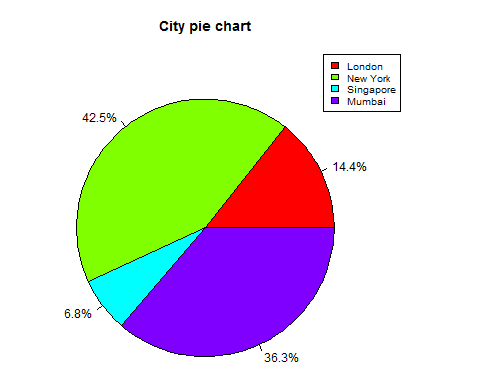
Slice Percentages and Chart Legend

We can add slice percentage and a chart legend by creating additional chart variables.

Live Demo

# Create data for the graph.
x <-  c(21, 62, 10,53)
labels <-  c("London","New York","Singapore","Mumbai")

piepercent<- round(100*x/sum(x), 1)

# Give the chart file a name.
png(file = "city_percentage_legends.jpg")

# Plot the chart.
pie(x, labels = piepercent, main = "City pie chart",col = rainbow(length(x)))
legend("topright", c("London","New York","Singapore","Mumbai"), cex = 0.8,
   fill = rainbow(length(x)))

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

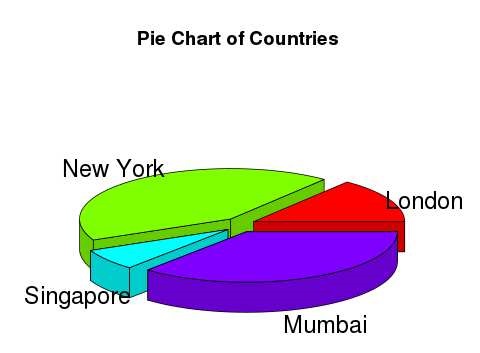
3D Pie Chart

A pie chart with 3 dimensions can be drawn using additional packages. The package plotrix has a function called pie3D() that is used for this.

# Get the library.
library(plotrix)

# Create data for the graph.
x <-  c(21, 62, 10,53)
lbl <-  c("London","New York","Singapore","Mumbai")

# Give the chart file a name.
png(file = "3d_pie_chart.jpg")

# Plot the chart.
pie3D(x,labels = lbl,explode = 0.1, main = "Pie Chart of Countries ")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

R - Boxplots

Boxplots are a measure of how well distributed is the data in a data set. It divides the data set into three quartiles. This graph represents the minimum, maximum, median, first quartile and third quartile in the data set. It is also useful in comparing the distribution of data across data sets by drawing boxplots for each of them.

Boxplots are created in R by using the boxplot() function.

Syntax

The basic syntax to create a boxplot in R is −

boxplot(x, data, notch, varwidth, names, main)

Following is the description of the parameters used −

• x is a vector or a formula.

• data is the data frame.

• notch is a logical value. Set as TRUE to draw a notch.

• varwidth is a logical value. Set as true to draw width of the box proportionate to the sample size.

• names are the group labels which will be printed under each boxplot.

• main is used to give a title to the graph.

Example

We use the data set "mtcars" available in the R environment to create a basic boxplot. Let's look at the columns "mpg" and "cyl" in mtcars.

Live Demo

input <- mtcars[,c('mpg','cyl')]
print(head(input))

When we execute above code, it produces following result −

                   mpg  cyl
Mazda RX4         21.0   6
Mazda RX4 Wag     21.0   6
Datsun 710        22.8   4
Hornet 4 Drive    21.4   6
Hornet Sportabout 18.7   8
Valiant           18.1   6

Creating the Boxplot

The below script will create a boxplot graph for the relation between mpg (miles per gallon) and cyl (number of cylinders).

Live Demo

# Give the chart file a name.
png(file = "boxplot.png")

# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, xlab = "Number of Cylinders",
   ylab = "Miles Per Gallon", main = "Mileage Data")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

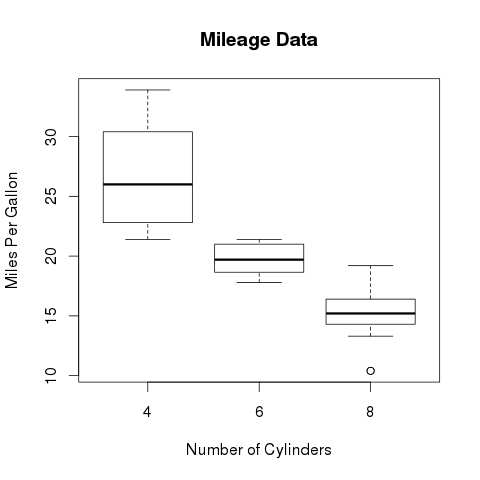
Boxplot with Notch

We can draw boxplot with notch to find out how the medians of different data groups match with each other.

The below script will create a boxplot graph with notch for each of the data group.

Live Demo

# Give the chart file a name.
png(file = "boxplot_with_notch.png")

# Plot the chart.
boxplot(mpg ~ cyl, data = mtcars, 
   xlab = "Number of Cylinders",
   ylab = "Miles Per Gallon", 
   main = "Mileage Data",
   notch = TRUE, 
   varwidth = TRUE, 
   col = c("green","yellow","purple"),
   names = c("High","Medium","Low")
)
# Save the file.
dev.off()

When we execute the above code, it produces the following result −

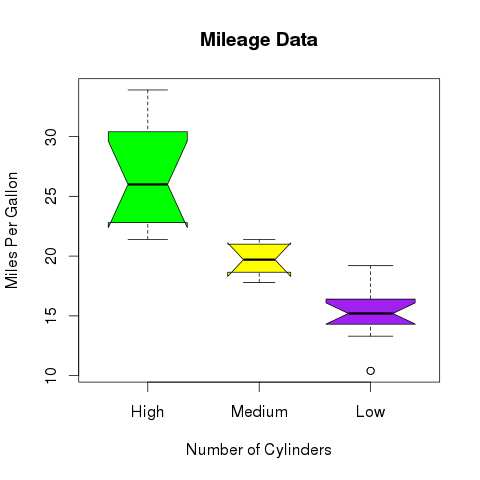
R - Histograms

A histogram represents the frequencies of values of a variable bucketed into ranges. Histogram is similar to bar chat but the difference is it groups the values into continuous ranges. Each bar in histogram represents the height of the number of values present in that range.

R creates histogram using hist() function. This function takes a vector as an input and uses some more parameters to plot histograms.

Syntax

The basic syntax for creating a histogram using R is −

hist(v,main,xlab,xlim,ylim,breaks,col,border)

Following is the description of the parameters used −

• v is a vector containing numeric values used in histogram.

• main indicates title of the chart.

• col is used to set color of the bars.

• border is used to set border color of each bar.

• xlab is used to give description of x-axis.

• xlim is used to specify the range of values on the x-axis.

• ylim is used to specify the range of values on the y-axis.

• breaks is used to mention the width of each bar.

Example

A simple histogram is created using input vector, label, col and border parameters.

The script given below will create and save the histogram in the current R working directory.

Live Demo

# Create data for the graph.
v <-  c(9,13,21,8,36,22,12,41,31,33,19)

# Give the chart file a name.
png(file = "histogram.png")

# Create the histogram.
hist(v,xlab = "Weight",col = "yellow",border = "blue")

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

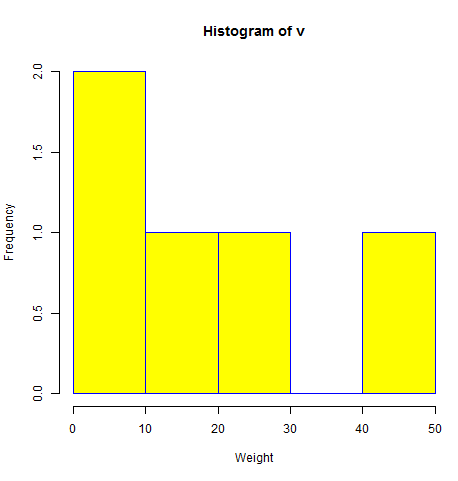
Range of X and Y values

To specify the range of values allowed in X axis and Y axis, we can use the xlim and ylim parameters.

The width of each of the bar can be decided by using breaks.

Live Demo

# Create data for the graph.
v <- c(9,13,21,8,36,22,12,41,31,33,19)

# Give the chart file a name.
png(file = "histogram_lim_breaks.png")

# Create the histogram.
hist(v,xlab = "Weight",col = "green",border = "red", xlim = c(0,40), ylim = c(0,5),
   breaks = 5)

# Save the file.
dev.off()

When we execute the above code, it produces the following result −

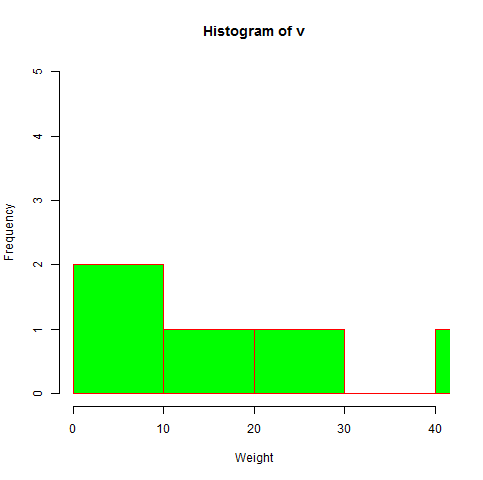
R - Scatterplots

Scatterplots show many points plotted in the Cartesian plane. Each point represents the values of two variables. One variable is chosen in the horizontal axis and another in the vertical axis.

The simple scatterplot is created using the plot() function.

Syntax

The basic syntax for creating scatterplot in R is −

plot(x, y, main, xlab, ylab, xlim, ylim, axes)

Following is the description of the parameters used −

• x is the data set whose values are the horizontal coordinates.

• y is the data set whose values are the vertical coordinates.

• main is the tile of the graph.

• xlab is the label in the horizontal axis.

• ylab is the label in the vertical axis.

• xlim is the limits of the values of x used for plotting.

• ylim is the limits of the values of y used for plotting.

• axes indicates whether both axes should be drawn on the plot.

Example

We use the data set "mtcars" available in the R environment to create a basic scatterplot. Let's use the columns "wt" and "mpg" in mtcars.

Live Demo

input <- mtcars[,c('wt','mpg')]
print(head(input))

When we execute the above code, it produces the following result −

                    wt      mpg
Mazda RX4           2.620   21.0
Mazda RX4 Wag       2.875   21.0
Datsun 710          2.320   22.8
Hornet 4 Drive      3.215   21.4
Hornet Sportabout   3.440   18.7
Valiant             3.460   18.1

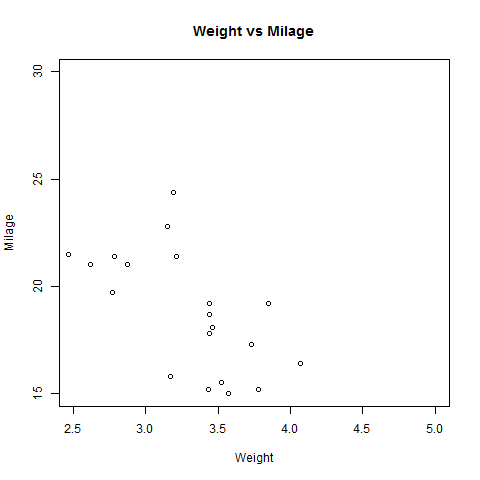
Creating the Scatterplot

The below script will create a scatterplot graph for the relation between wt(weight) and mpg(miles per gallon).

Live Demo

# Get the input values.
input <- mtcars[,c('wt','mpg')]

# Give the chart file a name.
png(file = "scatterplot.png")

# Plot the chart for cars with weight between 2.5 to 5 and mileage between 15 and 30.
plot(x = input$wt,y = input$mpg,
   xlab = "Weight",
   ylab = "Milage",
   xlim = c(2.5,5),
   ylim = c(15,30),		 
   main = "Weight vs Milage"
)
	 
# Save the file.
dev.off()

When we execute the above code, it produces the following result −

Scatterplot Matrices

When we have more than two variables and we want to find the correlation between one variable versus the remaining ones we use scatterplot matrix. We use pairs() function to create matrices of scatterplots.

Syntax

The basic syntax for creating scatterplot matrices in R is −

pairs(formula, data)

Following is the description of the parameters used −

• formula represents the series of variables used in pairs.

• data represents the data set from which the variables will be taken.

Example

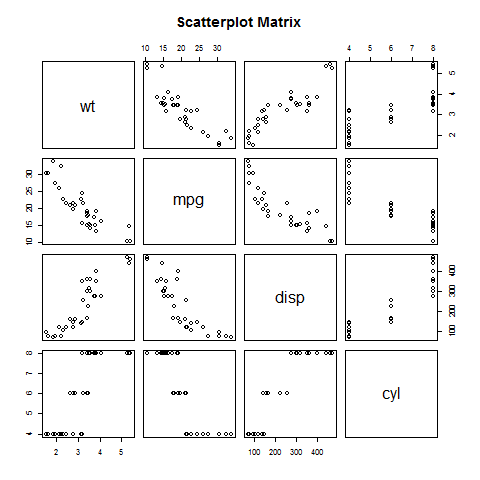
Each variable is paired up with each of the remaining variable. A scatterplot is plotted for each pair.

Live Demo

# Give the chart file a name.
png(file = "scatterplot_matrices.png")

# Plot the matrices between 4 variables giving 12 plots.

# One variable with 3 others and total 4 variables.

pairs(~wt+mpg+disp+cyl,data = mtcars,
   main = "Scatterplot Matrix")

# Save the file.
dev.off()

When the above code is executed we get the following output.